Effective Concurrency with Algebraic Effects

Algebraic effects and handlers provide a modular abstraction for expressing effectful computation, allowing the programmer to separate the expression of an effectful computation from its implementation. In this post, I will present an extension to OCaml for programming with linear algebraic effects, and demonstrate its use in expressing concurrency primitives for multicore OCaml. The design and implementation of algebraic effects for multicore OCaml is due to Leo White, Stephen Dolan and the multicore team at OCaml Labs.

Motivation

Multicore-capable functional programming language implementations such as Glasgow Haskell Compiler, F#, Manticore and MultiMLton expose one or more libraries for expressing concurrent programs. The concurrent threads of execution instantiated through the library are in turn multiplexed over the available cores for speed up. A common theme among such runtimes is that the primitives for concurrency along with the concurrent thread scheduler is baked into the runtime system. Over time, the runtime system itself tends to become a complex, monolithic piece of software, with extensive use of locks, condition variables, timers, thread pools, and other arcana. As a result, it becomes difficult to maintain existing concurrency libraries, let alone add new ones. Such lack of malleability is particularly unfortunate as it prevents developers from experimenting with custom concurrency libraries and scheduling strategies, preventing innovation in the ecosystem. Our goal with this work is to provide a minimal set of tools with which programmers can implement new concurrency primitives and schedulers as OCaml libraries.

A Taste of Effects

A Simple Scheduler

Let us illustrate the algebraic effect extension in multicore OCaml by constructing a concurrent round-robin scheduler with the following interface:

(* Control operations on threads *)
val fork  : (unit -> unit) -> unit
val yield : unit -> unit
(* Runs the scheduler. *)
val run   : (unit -> unit) -> unit

The basic tenet of programming with algebraic effects is that performing an effectful computation is separate from its interpretation¹. In particular, the interpretation is dynamically chosen based on the context in which an effect is performed. In our example, spawning a new thread and yielding control to another are effectful actions, for which we declare the following effects:

type _ eff +=
| Fork  : (unit -> unit) -> unit eff
| Yield : unit eff

The type 'a eff is the predefined extensible variant type for effects, where 'a represents the return type of performing the effect. For convenience, we introduce new syntax using which the same declarations are expressed as follows:

effect Fork  : (unit -> unit) -> unit
effect Yield : unit

Effects are performed using the primitive perform of type 'a eff -> 'a. We define the functions fork and yield as follows:

let fork f = perform (Fork f)
let yield () = perform Yield

What is left is to provide an interpretation of what it means to perform fork and yield. This interpretation is provided with the help of handlers.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
let run main =
  let run_q = Queue.create () in
  let enqueue k = Queue.push k run_q in
  let rec dequeue () =
    if Queue.is_empty run_q then ()
    else continue (Queue.pop run_q) ()
  in
  let rec spawn f =
    match f () with
    | () -> dequeue ()
    | exception e ->
        print_string (to_string e);
        dequeue ()
    | effect Yield k ->
        enqueue k; dequeue ()
    | effect (Fork f) k ->
        enqueue k; spawn f
  in
  spawn main

The function spawn f (line 8) evaluates f in a new thread of control. f may return normally with value () or exceptionally with an exception e or effectfully with the effect performed along with the delimited continuation² k. In the pattern effect e k, if the effect e has type 'a eff, then the delimited continuation k has type ('a,'b) continuation, i.e., the return type of the effect 'a matches the argument type of the continuation, and the return type of the delimited continuation is 'b.

Observe that we represent the scheduler queue with a queue of delimited continuations, with functions to manipulate the queue (lines 2–6). In the case of normal or exceptional return, we pop the scheduler queue and resume the resultant continuation using the continue primitive (line 6). continue k v resumes the continuation k : ('a,'b) continuation with value v : 'a and returns a value of type 'b. In the case of effectful return with Fork f effect (lines 16–17), we enqueue the current continuation to the scheduler queue and spawn a new thread of control for evaluating f. In the case of Yield effect (lines 14–15), we enqueue the current continuation, and resume some other saved continuation from the scheduler queue.

Testing the scheduler

Lets write a simple concurrent program that utilises this scheduler, to create a binary tree of tasks. The sources for this test are available here. The program concurrent.ml:

let log = Printf.printf

let rec f id depth =
  log "Starting number %i\n%!" id;
  if depth > 0 then begin
    log "Forking number %i\n%!" (id * 2 + 1);
    Sched.fork (fun () -> f (id * 2 + 1) (depth - 1));
    log "Forking number %i\n%!" (id * 2 + 2);
    Sched.fork (fun () -> f (id * 2 + 2) (depth - 1))
  end else begin
    log "Yielding in number %i\n%!" id;
    Sched.yield ();
    log "Resumed number %i\n%!" id;
  end;
  log "Finishing number %i\n%!" id

let () = Sched.run (fun () -> f 0 2)

generates a binary tree of depth 2, where the tasks are numbered as shown below:

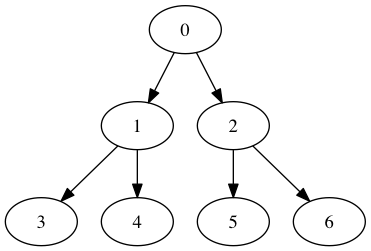
The program forks new tasks in a depth-first fashion and yields when it reaches maximum depth, logging the actions along the way. To run the program, first install multicore OCaml compiler, available from the OCaml Labs dev repo. Once the compiler is installed, the above test program can be compiled and run as follows:

$ git clone https://github.com/kayceesrk/ocaml-eff-example
$ cd ocaml-eff-example
$ make
$ ./concurrent
Starting number 0
Forking number 1
Starting number 1
Forking number 3
Starting number 3
Yielding in number 3
Forking number 2
Starting number 2
Forking number 5
Starting number 5
Yielding in number 5
Forking number 4
Starting number 4
Yielding in number 4
Resumed number 3
Finishing number 3
Finishing number 0
Forking number 6
Starting number 6
Yielding in number 6
Resumed number 5
Finishing number 5
Finishing number 1
Resumed number 4
Finishing number 4
Finishing number 2
Resumed number 6
Finishing number 6

The output illustrates how the tasks are forked and scheduled.

Implementation

Fibers for Concurrency

The main challenge in the implementation of algebraic effects is the efficient management of delimited continuations. In multicore OCaml³, the delimited continuations are implemented using fibers, which are small heap-allocated, dynamically resized stacks. Fibers represent the unit of concurrency in the runtime system.

Our continuations are linear (one-shot)⁴, in that once captured, they may be resumed at most once. Capturing a one-shot continuation is fast, since it involves only obtaining a pointer to the underlying fiber, and requires no allocation. OCaml uses a calling convention without callee-save registers, so capturing a one-shot continuation requires saving no more context than that necessary for a normal function call.

Since OCaml does not have linear types, we enforce the one-shot property at runtime by raising an exception the second time a continuation is invoked. For applications requiring true multi-shot continuations (such as probabilistic programming⁵), we envision providing an explicit operation to copy a continuation.

While continuation based concurrent functional programming runtimes such as Manticore and MultiMLton use undelimited continuations, our continuations are delimited. We believe delimited continuations enable complex nested and hierarchical schedulers to be expressed more naturally due to the fact that they introduce parent-child relationship between fibers similar to a function invocation.

Running on Multiple Cores

Multicore OCaml provides support for shared-memory parallel execution. The unit of parallelism is a domain, each running a separate system thread, with a relatively small local heap and a single shared heap shared among all of the domains. In order to distributed the fibers amongst the available domains, work sharing/stealing schedulers are initiated on each of the domains. The multicore runtime exposes to the programmer a small set of locking and signalling primitives for achieving mutual exclusion and inter-domain communication.

The multicore runtime has the invariant that there are no pointers between the domain local heaps. However, the programmer utilising the effect library to write schedulers need not be aware of this restriction as fibers are transparently promoted from local to shared heap on demand. We will have to save multicore-capable schedulers for another post.